Introduction to Analog and Digital Signals
In everyday life, most of the signals we encounter are analog signals. To store real-world information—such as weather phenomena like wind, rain, thunder, and lightning, the sounds we hear, or the temperature changes we feel—into a computer, a series of processing steps are required. One crucial step is the conversion from analog signals to digital signals, commonly referred to as analog-to-digital conversion (A/D conversion).
Suppose there actually exists a 1 kHz sound wave signal. If we want to receive and process this signal, we must first perform analog-to-digital conversion. We cannot directly store this analog signal on a computer because analog signals are continuous, and continuous signals cannot be stored in digital systems. Therefore, the transformation from analog to digital signals forms the foundation for all computer-based data and signal processing. In computers, A/D conversion is achieved through sampling and quantization. Specifically, the analog signal is first converted into an electrical signal (e.g., a voltage signal), which is then sampled and quantized to produce a digital signal. Note that this process involves two key steps: first, transforming the physical signal into an electrical signal—this is the basis of signal processing. However, even after this transformation, the signal remains continuous. The second step involves sampling the electrical signal over time and then quantizing the sampled values.
In the context of audio signal processing, we first use a microphone to capture sound waves. This capturing process refers specifically to the microphone's ability to convert the analog sound wave into a voltage signal. As shown in the figure below, the microphone contains a thin diaphragm that vibrates in response to sound. These vibrations cause continuous variations in voltage, so the changing voltage represents the variation in the sound wave.
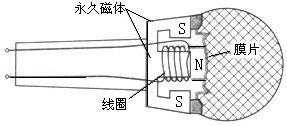
However, it's important to note that after the microphone converts the sound wave into a voltage signal, this voltage signal remains continuous both in time and in amplitude. Theoretically, the voltage can take any real value within its range, and it varies continuously over time. Clearly, such continuous data cannot be stored directly in a computer—it would require infinite storage space.
Think about why a signal that is continuous in time would require infinite storage space?
To store such data, we must first process it. The first step is converting the signal that is continuous in time into one that is discrete in time. This is achieved through sampling. Sampling means that the device periodically measures the voltage signal. "Periodic measurement" typically means measurements taken at fixed time intervals. The number of samples taken per second is called the sampling frequency, or sampling rate, measured in hertz (Hz).
This raises a critical question: How high should the sampling rate be? How do we determine the optimal sampling frequency? We will discuss this in detail in the section on Signal Sampling and the Sampling Theorem.
Even after sampling, the voltage values still cannot be stored directly because the voltage values themselves remain continuous within their possible range. Thus, even sampled voltage values would theoretically require infinite storage space.
Think about why a signal with continuous amplitude values would require infinite storage space?
To solve this problem, we need to quantize the signal. Simply put, quantization converts the infinite, continuous range of voltage values into a finite set of discrete values. Only after both sampling and quantization can we truly store the audio signal in a digital system. The device we commonly refer to as an Analog-to-Digital Converter (ADC) performs exactly this function. Conversely, a Digital-to-Analog Converter (DAC) performs the reverse operation.
Similarly, to play back a sound wave stored in a computer, we need the inverse process of A/D conversion: digital-to-analog conversion (D/A conversion). Take a loudspeaker (or speaker) as an example: the speaker receives digital audio data from the computer, which is converted by a DAC into an analog electrical signal. This electrical signal drives the motion of an electromagnet, which in turn causes the speaker’s diaphragm to vibrate, thereby reproducing the sound wave. The actual process of wireless data transmission follows a similar principle: data is converted by communication devices into electromagnetic wave signals, which are then transmitted through space.
How quantization is performed and what effects it has will be discussed in detail in the upcoming section on Signal Quantization.